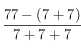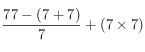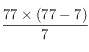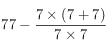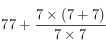L’expérience ici présentée est un peu inhabituelle pour moi : il s’agit d’une partition purement conceptuelle, qui n’a (à ma connaissance) jamais été jouée et n’est d’ailleurs pas destinée à l’être. Elle n’existe que sous forme manuscrite, et je n’ai eu que le temps de la photographier hâtivement après l’avoir offerte à son dédicataire, le compositeur américain Tom Johnson. (Dans les photos détaillées, l’on pourra d’ailleurs voir quelques bouts de la nappe de sa table à manger.)
Véritable pastiche oumupien (Tom ayant récemment accepté de rejoindre l’Oumupo que j’ai refondé et que j’anime depuis 2011), cette partition ne doit pas être prise trop au sérieux, sauf peut-être à un égard : elle est en fait la stricte traduction sous forme musicale1 des solutions proposées par Georges Perec à un problème arithmétique qu’il avait lui-même imaginé :
En utilisant 7 fois le chiffre 7, pas une fois de plus, pas une fois de moins, et les signes mathématiques les plus usuels, écrire les nombres de 1 à n.
Historique
[Cliquez pour déplier.]
Georges Perec
De tous les écrivains de l’Oulipo, aucun n’est plus connu (à juste titre, sans aucun doute) que Georges Perec. Sa renommée a éclipsé celle du co-fondateur de l’ouvroir (Raymond Queneau) et, bien plus encore, de son concepteur initial (François Le Lionnais, à qui j’ai d’ailleurs récemment consacré un podcast). On lui consacre des traductions, des émissions, des colloques, en veux-tu en voilà — ce qui ne laisse pas de me chagriner car j’ai toujours nourri le rêve (secret et embarrassant) d’être moi-même le plus inconditionnel des fans de Perec : il est, à mon sens, l’écrivain français le plus essentiel de ces deux derniers siècles, voire (les jours où je suis grincheux) tout simplement le seul auteur du XXe siècle qui mérite d’être mentionné. Or voilà : au-delà de ses livres les plus connus (que je n’ai d’ailleurs même pas tous lus, du moins pas en entier), son œuvre comprend des objets fort variés, souvent inattendus, et parfois complètement oubliés.
Ainsi, ma femme m’offrit l’année dernière — pour mon propre anniversaire — un petit recueil (d’une centaine de pages à peine) où sont regroupés des jeux que Perec conçut entre 1981 et 1982 pour le magazine Jeune Afrique. Il s’agit ici de la toute fin de sa vie (les derniers de ces jeux sont envoyés par Jacques Bens en février 1982, et Perec mourra le 3 mars). Parmi les jeux proposés, se trouve cette série de « Avec sept “7” », dont l’énoncé figure plus haut ; il s’agit d’un jeu mathématique relativement classique (on en trouve par exemple une variante avec quatre 4), même si le nombre 7 fait évidemment partie des nombres qu’affectionne Perec (de même que 11 ou 43, pour des raisons plus personnelles).
J’ai regardé attentivement ce petit livre (non sans me reporter abondamment et honteusement aux pages de solutions incluses vers la fin), puis l’ai rangé et n’y ai plus pensé. Jusqu’à ce que...
Tom qui ?
Lorsque j’ai fondé l’Oumupo actuel en 2011, je connaissais vaguement l’existence d’un compositeur américain du nom de Tom Johnson ; je n’avais sans doute rien entendu de lui, mais je connaissais de nom quelques-unes de ses expériences musicales. Des titres tels que The Four Notes Opera ne pouvaient que m’être sympathiques, même si je les imaginais cantonnés aux années 1960-70, et ne me posais de ce fait aucune autre question. Du reste, les exemples d’influences oumupiennes, historiques ou actuelles, ne manquaient pas (et si j’avais dû y mentionner Tom Johnson, je l’aurais sans doute fait parmi celles-là plutôt que parmi celles-ci).
Or quelques mois plus tard, j’eus la surprise de constater (je n’aurais pas été surpris si j’avais fait mes devoirs au préalable, mais ne sous-estimons jamais mon degré d’amateurisme) que le dénommé Tom Johnson
- était encore en vie
- était encore en activité
- se trouvait en France en ce moment
(j’appris plus tard qu’il vivait en fait à Paris depuis trente ans) - et était l’invité de l’Oulipo lors de la lecture publique du jeudi 9 février 2012, de 19 heures à 20 heures.
“Tiens”, me dis-je. “Peut-être serait-il intéressant d’y assister, pour une fois, plutôt que d’arriver à 19h58 pour pouvoir faire semblant d’avoir été présent tout le long, et aller ensuite manger (voracement) une pizza avec les habitués du public.”
Le jour venu, je me préparai à l’avance. Longuement. Et j’arrivai, consciencieusement, non pas à 19h58.
Mais à 19h55.
(Je vous le disais : ne sous-estimons jamais mon degré d’indécrottable amateurisme.)
J’eus tout au plus le temps d’entendre ledit Tom Johnson présenter l’une de ses expériences, puis la jouer au piano — une phrase unique, répétée chaque fois un peu plus longuement, des méandres s’y ajoutant de façon presque envoûtante.
“Tiens”, me dis-je.
Tom Johnson
Tom Johnson est un authentique compositeur minimaliste américain. Le mouvement minimaliste — parfois aussi dénommé, non sans raison, « musique répétitive » — est un courant de la deuxième moitié du XXe siècle (on l’associera parfois aux sérigraphies du Pop Art, et il est vrai qu’il partage avec cet autre courant un certain aspect accessible, voire facile ou branché). À une époque où l’Europe s’engluait passablement dans l’hyper-complexité, le sérialisme intégral et le boulézianisme galopant, ce courant a fourni une façon de recycler les éléments musicaux du passé (notes, harmonies) dans une approche séduisante, accessible à un large public et en même temps très moderne (d’aucuns diraient « post-moderne ») pour l’époque.
Et pourtant : force nous est de reconnaître que, passé l’emballement que provoquent quelques œuvres de jeunesses de Steve Reich (surtout) et Philip Glass (un peu), ces objets musicaux vieillissent assez mal. D’ailleurs, les ci-devants compositeurs répétitifs eux-même ont très rapidement renoncé aux aspects les plus expérimentaux de leur démarche, et se sont retrouvés entièrement digérés dans l’énorme machine des prescripteurs industriels et politiques mainstream qui cherche constamment à légitimer comme « savants » et « contemporains » des objets artistiques en réalité essentiellement réactionnaires.
Or voilà : Tom Johnson est exactement de la génération de ces gens-là (il est même leur camarade de tranchée, à l’origine) — et pourtant : lui, n’a absolument rien perdu de sa radicalité. Au contraire : il s’est élevé, au fil des décennies, vers une quête presque platonicienne où les contingences de la musique n’existent plus : seul compte le principe générateur, qu’il s’agisse d’un automate algorithmique, d’une formule ou d’une démarche intellectuelle. L’objet se déploie de lui-même, et l’auteur ne cherche qu’à le mettre en valeur (sans artifices ni roublardise), voire se limite à un simple rôle de témoin naïf. Il s’agit donc de musique conceptuelle, mais — plus étonnant encore — d’une musique conceptuelle qui vieillit exceptionnellement bien ; peut-être parce que l’humour y est parfois perceptible.
De tout cela, les derniers instants de la conférence du 9 février 2012 m’ont suffi pour avoir l’intuition. Alors que le public progressait vers la sortie, je descendis vers la scène à la rencontre de ce vieux monsieur auquel plus personne ne semblait s’intéresser ; me pourvoyant mentalement de mon masque souriant pour dissimuler tout ce que ce moment avait d’embarrassant, je lui serrai la main en livrant quelques formules convenues de salutations élogieuses. (C’est alors qu’il m’apprit qu’il vivait en fait à Paris, où il avait même fondé sa propre maison d’édition.) Pas un instant ne me vint la tentation de lui parler de l’Oumupo, qui ne comptait alors que deux membres et n’avait pas la moindre existence officielle, en-dehors de son site Web codé par mes soins. (Non que la situation soit si différente aujourd’hui.)
Un mois plus tard, pourtant (lors de la soirée suivante de l’Oulipo le jeudi 22 mars 2012), l’Oumupo (fort désormais de trois membres !) faisait ses débuts en public. Et dans nos discussions subséquentes revint dès lors, chaque année, la même question : « au fait, quand est-ce qu’on se décidera à proposer à Tom Johnson de nous rejoindre » ?
Tom Johnson à l’Oumupo
En 2016, notre membre le plus récent (mais pas le moins sympathique, malgré sa sujétion à l’Ircam), Moreno Andreatta, mentionna qu’il connaissait bien Tom Johnson, pour l’avoir invité à ses sauteries universitaires à thème « maths et musique ». Il proposa de faire l’entremise ; je l’acceptai après quelques ultimes tergiversations, non sans garder conscience de l’arrogance de notre démarche : en matière d’écriture musicale sous contraintes, l’Oumupo que j’avais voulu (re)lancer n’était qu’un piètre essai de réinventage de roue en comparaison de la carrière toute entière de Tom Johnson. Mais — me dis-je — ce serait peut-être, tout de même, une possibilité d’acquérir un peu de légitimité symbolique, en nous plaçant sous son parrainage. Je l’imaginais en « membre d’honneur », en Père Noël oumupien que nous ne côtoierions jamais mais dont nous serions contents de savoir qu’il existe.
Or, nouvelle surprise : non seulement ledit Tom Johnson accepta notre invitation avec empressement, mais il n’avait aucune envie de jouer les Reines d’Angleterre. Au contraire, sa plus grande envie était de venir jouer dans le bac à sable avec nous, et — même s’il est encore tôt pour l’estimer — j’espère que son arrivée aura été aussi stimulante pour lui que pour nous. De fait, si le domaine des mathématiques est son empire, l’état d’esprit oulipien et ou-x-pien reste pour lui un objet nouveau, et j’ai cru comprendre que les expérimentations de Le Lionnais, Queneau puis tous les autres (qu’il commence tout juste à découvrir, par mon intermédiaire) lui fourniront peut-être une source d’inspiration conséquente pour les années à venir.
En tout cas, c’est certainement la rencontre la plus marquante qu’il m’ait été donné de faire dernièrement. À l’Oumupo, j’avais toujours été le grincheux de service, le bureaucrate-crispé au milieu d’une bande de joyeux fantaisistes ; or le sérieux, la rigueur et l’intégrité de Tom Johnson sont sans commune mesure. Je me souviendrai toujours de la première fois où je suis allé le rencontrer chez lui rue de la Roquette. Croyant trouver parmi mes partitions quelque chose dans lequel il se reconnaîtrait, je lui avais apporté mes petites études potentielles, partition assez austère entièrement générée par un carré latin. Je m’assis au piano et commençai à jouer... je n’avais pas entamé la troisième mesure que Tom Johnson me demanda doucement :
— Je ne comprends pas : pourquoi vous avez mis des nuances ?
Moi, désemparé : « euh... eh bien justement, c’est pour que malgré l’écriture mathématique, il y ait de l’expressivité, du sens ; c’est important, je crois ? D’ailleurs, les musiciens qui jouent vos partitions, ils ajoutent bien des nuances, non ? »
— Mais ça, ce sont les mauvais musiciens qui ajoutent des nuances ; moi je ne mets pas de nuances ; je laisse ça aux compositeurs romantiques.
En rentrant chez moi, plus tard, j’étais toujours aussi déconcerté.
De toute ma carrière — et c’est assurément un bien grand mot — on m’a qualifié de nombreuses façons (qui se confondent, il est vrai, avec les anathèmes que je me suis moi-même lancés in petto). Intello, hermétique, sophistiqué, inutilement complexe, pas-entendu, maladroit, bavard, imbu de lui-même, facile, soupe, hollywoodien, fanfaron,... Romantique ? Jamais.
Et pourtant : alors que je marchais dans la rue, je constatai avec surprise que mon pas était soudain devenu plus allègre que de coutume.
Description
[Cliquez pour déplier.]
Le 18 novembre 2016, Tom Johnson était destiné à fêter ses 77 ans. Pour un maniaque du chiffre, un tel nombre ne peut laisser indifférent — et d’ailleurs, Tom lui-même a tenu à marquer le coup en rédigeant Sept septuors sous des contraintes très réussies.
Pour moi, 7 reste avant tout le nombre de notes dans la gamme diatonique : les touches blanches du piano.2 J’ai d’ailleurs beaucoup utilisé l’espace de hauteurs diatoniques, que ce soit dans mes « études potentielles » précitées, dans mes sonates pour piano et pour flûte ou plus récemment dans quelques variations pour quatuor à cordes.
Il serait donc (potentiellement — c’est le mot) intéressant de jouer 7 fois les 7 notes, de façons différentes. Et c’est là que les sept “7” de Perec me revinrent à l’esprit.
Disposant d’équations et d’un motif mélodique (la simple gamme do-ré-mi-fa-sol-la-si), il ne me restait plus qu’à chercher une façon d’effectuer la traduction. Là où Tom Johnson aurait probablement emprunté la voie arithmétique (ce qui l’aurait conduit, par exemple, à exprimer « 7×7 » en jouant 49 notes), je choisis d’effectuer une pure translittération, en me fixant les règles — arbitraires — suivantes :
- n’utiliser que des séquences diatoniques, de
doàsi(soit : 7 notes). - additions : par défaut, les mouvements mélodiques sont ascendants (dans le cas de nombres positifs et d’additions).
- soustractions : le signe « moins » est exprimé par une mélodie descendante ; si toute une expression est négative, dans ce cas tous les mouvements mélodiques lui correspondant sont renversés.
- multiplications : le premier terme est joué normalement, puis le facteur multipliant est joué deux fois plus vite et une octave plus haut. (Il peut arriver que des multiplications s’enchâssent.)
- divisions et fractions : le numérateur est joué normalement ; le diviseur ou dénominateur est joué à une octave inférieure et avec des valeurs plus longues. Si c’est une vraie division, le rythme du dénominateur doit correspondre à la durée totale des notes contenues dans le numérateur, de façon à ce que les deux voix finissent au même moment. Dans le cas d’une fraction égale à 1 (7/7, 77/77 etc.) le dénominateur, c’est-à-dire la voix du bas, restera toutefois plus lent que le numérateur, et finit de ce fait nettement plus tard que la voix du haut. (Dans le cas de rythmes trop compliqués, les notations ont été simplifiées.)
- L’écriture de la partition suit la notation mathématique sans tenir compte de sa signification : ainsi, seules les fractions sont restituées sous forme polyphonique car sur le papier ce sont les seules notations écrites sur plusieurs lignes.
- les expressions entre parenthèses sont exprimées par l’emploi de la pédale. (J’en ai omises quelques-unes.)
- les puissances (exposants) sont exprimés par des appoggiatures barrées (donc très rapides), à l’octave la plus haute possible.
- toute la notation rythmique a été simplifiée ; une pulsation constante est employée, et certaines valeurs rythmiques ont été légèrement retouchées de façon à préserver la partition d’un aspect trop inutilement compliqué.
En théorie, il est donc possible d’effectuer l’opération inverse : en partant seulement de la partition, retrouver quelle opération a été posée par Perec pour arriver à obtenir le nombre requis en n’écrivant que sept fois le chiffre 7, à l’exclusion de tout autre. À l’énigme mathématique se substitue alors un puzzle musical ; l’idée n’aurait peut-être pas déplu à l’intéressé... et de fait, la partition se suffit alors à elle-même.
Mais comme je suis sympa, j’ai quand même recopié les solutions en clair ci-dessous.
Solutions
[Cliquez pour déplier.]
Voici les solutions proposées par Georges Perec pour compter de 1 à 90 ; dans ma partition toutefois, je ne vais que de 1 à 77.
Avec sept « 7 » (Georges Perec.)
1=
2=
3=
4=
5=
6=
7=
8=
9=
10=
11=
12=
13=
14=
15=
16=
17=
18=
19=
20=
21=
22=
23=
24=
25=
26=
27=
28=
29=
30=
31=
32=
33=
34=
35=
36=
37=
38=
39=
40=
41=
42=
43=
44=
45=
46=
47=
48=
49=
50=
51=
52=
53=
54=
55=
56=
57=
58=
59=
60=
61=
62=
63=
64=
65=
66=
67=
68=
69=
70=
71=
72=
73=
74=
75=
76=
77=
78=
79=
80=
81=
82=
83=
84=
85=
86=
87=
88=
89=
90=
 [Le Site]
[Le Site] Seven Sevens
Seven Sevens